1.

(1)
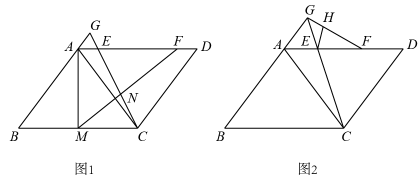
如图①,△AOB和△COD是等腰直角三角形,∠AOB=∠COD=90°,点C在OA上,点D在线段BO的延长线上,连接AD、BC.线段AD与BC的数量关系为
(2)
如图②,将图①中的△COD绕点O顺时针旋转a(0°<a<90°),第(1)问的结论是否仍然成立?如果成立,证明你的结论;若不成立,说明理由.
(3)
如图③,若AB=5,点C是线段AB外一动点,AC=3,连接BC,将CB绕点C逆时针旋转90°得到CD,连接AD,解答下列问题.
①当点C落在线段AD上时,AD的长为
②直接写出AD长度的最大值和最小值.
【考点】
三角形全等及其性质;
相似三角形的判定与性质;