1.
课本再现

(1)
在课本11.2.2章节中,我们学习了三角形内角和定理得出的推论:三角形的外角等于与它不相邻的两个内角的和.
(2)
如图3,线段 相交于点O,连接
相交于点O,连接 , 我们把形如这样的图形称为“8字型”.请仔细观察该图形,直接写出
, 我们把形如这样的图形称为“8字型”.请仔细观察该图形,直接写出 之间的数量关系 .
(3)
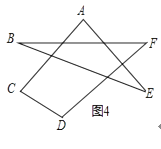
如图4,由线段组成的一个“风筝”形状,运用(2)中得出的数量关系,解答下列问题.
之间的数量关系 .
(3)
如图4,由线段组成的一个“风筝”形状,运用(2)中得出的数量关系,解答下列问题.
已知:是
的一个外角(如图1).求证:
.
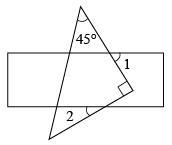
证明:如图2,过点C作 . (请完成后面的证明)
①试比较与
的大小,并说明理由;
②若 , 则
▲ .
【考点】
平行线的性质;
三角形内角和定理;
三角形的外角性质;
对顶角及其性质;