1.
综合实践课上,小聪把一张长方形纸片ABCD沿着虚线EB剪开,如图①所示,把得到的两张纸片如图②摆放,纸片Rt△CB′E′较小锐角的顶点E′在DE上,较长直角边与斜边分别交边AB于点G,H.以点G与A重合,且B′E′⊥LAB为初始位置,把Rt△CB′E′沿着DE方向平移,当点E′到达点E后立刻绕点E逆时针旋转,如图③,直到点H与点B重合停止.为了探求BH与AG之间的变化关系,设AG=m,请用含m的代数式表示BH.
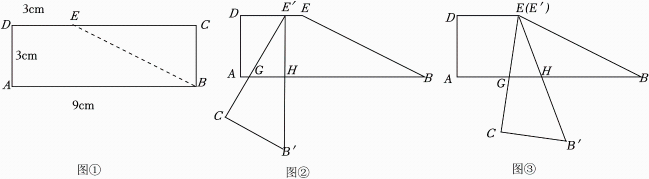
(1)
在平移过程中,BH=,
(2)
在旋转过程中,BH=.
【考点】
矩形的性质;
平移的性质;
相似三角形的判定与性质;
锐角三角函数的定义;
旋转的性质;