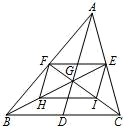
我们把依次连接任意一个四边形各边中点所得的四边形叫做中点四边形．如图，E、F、G、H分别是四边形各边的中点．

1. 我们把依次连接任意一个四边形各边中点所得的四边形叫做中点四边形．如图，E、F、G、H分别是四边形 $\text{[math]}$ 各边的中点．

(1) 求证：四边形 $\text{[math]}$ 是平行四边形；

(2) 如果我们对四边形 $\text{[math]}$ 的对角线 $\text{[math]}$ 与 $\text{[math]}$ 添加一定的条件，则可使四边形 $\text{[math]}$ 成为特殊的平行四边形，请你经过探究后直接填写答案：

①当 $\text{[math]}$ 时，四边形 $\text{[math]}$ 为；

②当 $\text{[math]}$ $\text{[math]}$ 时，四边形 $\text{[math]}$ 为矩形；

③当 $\text{[math]}$ 且 $\text{[math]}$ 时，四边形 $\text{[math]}$ 为．

【考点】

平行四边形的判定与性质; 菱形的判定; 矩形的判定; 正方形的判定; 三角形的中位线定理;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

综合题普通

综合题普通

综合题普通