1.
请用直尺、圆规作图,不写作法,但要保留作图痕迹.
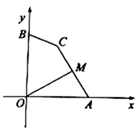
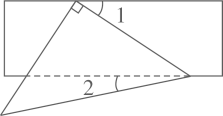
求作:以点为直角顶点的等腰直角三角形,使它的斜边落在直线
上,并在三角形内部做出以斜边中点为圆心的面积最大的半圆
.

【考点】
等腰直角三角形;
能力提升
变式训练
拓展培优
真题演练