1.
如图

(1)
回归教材:如图1,小然同学在学习九年级上(北师版)教材P90页时,遇到了这个问题.如图,在△ABC中, ,
,  , 垂足为D.求证:
, 垂足为D.求证: . 请你替小然写出过程.
(2)
小试牛刀:如图2,
. 请你替小然写出过程.
(2)
小试牛刀:如图2, ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
(3)
变式探索:如图3,△ABC中,
.
(3)
变式探索:如图3,△ABC中, , 点D为△ABC内部一点,且满足
, 点D为△ABC内部一点,且满足 ,
,  ,
,  ,
,  , 求AD长.
(4)
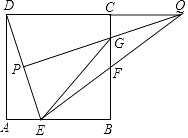
拓展应用:如图4,正方形ABCD中,以D为圆心,DC为半径作圆在正方形内得到弧AC,点P为弧AC上一点,且满足
, 求AD长.
(4)
拓展应用:如图4,正方形ABCD中,以D为圆心,DC为半径作圆在正方形内得到弧AC,点P为弧AC上一点,且满足 . △BPC面积记作
. △BPC面积记作 , 正方形ABCD面积记为
, 正方形ABCD面积记为 .
.
①求;②试猜想
与
的数量关系并证明.
【考点】
三角形的面积;
勾股定理;
正方形的性质;
相似三角形的判定与性质;
锐角三角函数的定义;
能力提升