1.
如图，直角△ABC中，∠A为直角，AB=6，AC=8．点P，Q，R分别在AB，BC，CA边上同时开始作匀速运动，2秒后三个点同时停止运动，点P由点A出发以每秒3个单位的速度向点B运动，点Q由点B出发以每秒5个单位的速度向点C运动，点R由点C出发以每秒4个单位的速度向点A运动，在运动过程中：
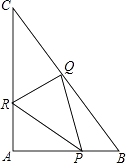
(1)
求证：△APR，△BPQ，△CQR的面积相等；
(2)
求△PQR面积的最小值；
(3)
用t（秒）（0≤t≤2）表示运动时间，是否存在t，使∠PQR=90°？若存在，请直接写出t的值；若不存在，请说明理由．
【考点】
二次函数的最值;
锐角三角函数的定义;
， sin15°=
）