1.
在平面直角坐标系中，点A坐标为（4，3），反比例函数y＝ 
（k＞0）的图象分别交矩形ABOC的两边AC，AB于点E，F（点E，F不与点A重合），沿着EF将△AEF折叠，点A落在点D处.
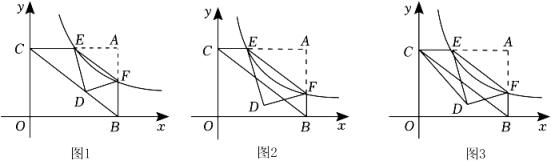
(1)
如图1，当点E为AC中点时，求点F的坐标，并直接写出EF与对角线BC的关系；
(2)
如图2，当点E位置发生改变时，EF与BC是否存在（1）中的位置关系，请说明理由；
(3)
如图3，连接CD，当CD平分∠ACO时，求出此时反比例函数的表达式.
【考点】
坐标与图形性质;
待定系数法求反比例函数解析式;
矩形的性质;
翻折变换（折叠问题）;
反比例函数图象上点的坐标特征;
