1.
在平面直角坐标系中,某个函数图象上任意两点的坐标分别为 和
和 (其中t为常数且
(其中t为常数且 ),将
),将 的部分沿直线
的部分沿直线 翻折,翻折后的图象记为
翻折,翻折后的图象记为 ;将
;将 的部分沿直线
的部分沿直线 翻折,翻折后的图象记为
翻折,翻折后的图象记为 , 将
, 将 和
和 及原函数图象剩余的部分组成新的图象G.
及原函数图象剩余的部分组成新的图象G.
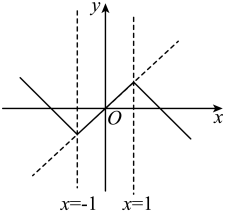
例如:如图,当时,原函数
, 图象G所对应的函数关系式为
.
(1)
当 时,原函数为
时,原函数为 , 图象G与坐标轴的交点坐标是.
(2)
对应函数
, 图象G与坐标轴的交点坐标是.
(2)
对应函数 (n为常数).
(n为常数).
①时,若图象G与直线
恰好有两个交点,求t的取值范围.
②当时,若图象G在
上的函数值y随x的增大而减小,直接写出n的取值范围.
【考点】
二次函数与一次函数的综合应用;
能力提升
真题演练