1.
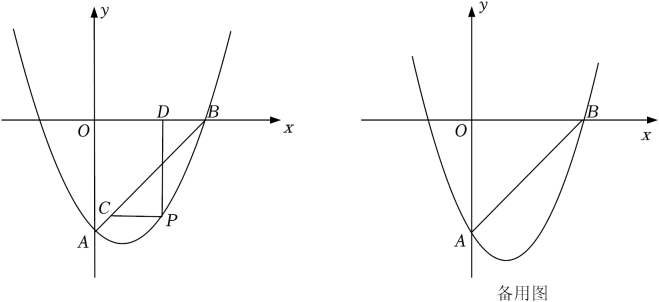
已知抛物线 (a,c为常数,
(a,c为常数, )经过点
)经过点 , 顶点为D.
, 顶点为D.
(1)
当 时,求该抛物线的对称轴,写出顶点D的坐标;
(2)
当
时,求该抛物线的对称轴,写出顶点D的坐标;
(2)
当 时,点
时,点 , 若
, 若 , 求该抛物线的解析式;
(3)
当
, 求该抛物线的解析式;
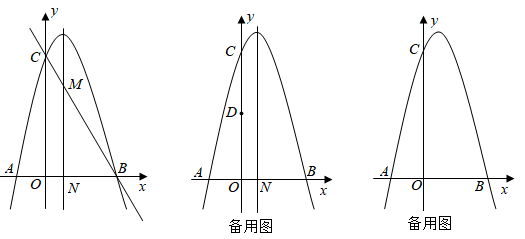
(3)
当 时,点
时,点 , 过点C作直线l平行于x轴,
, 过点C作直线l平行于x轴, 是x轴上的动点,
是x轴上的动点, 是直线l上的动点.试探究当a为何值时,
是直线l上的动点.试探究当a为何值时, 的最小值为
的最小值为 , 并求此时点M,N的坐标.
, 并求此时点M,N的坐标.
【考点】
待定系数法求二次函数解析式;
二次函数-动态几何问题;
能力提升
真题演练