1.
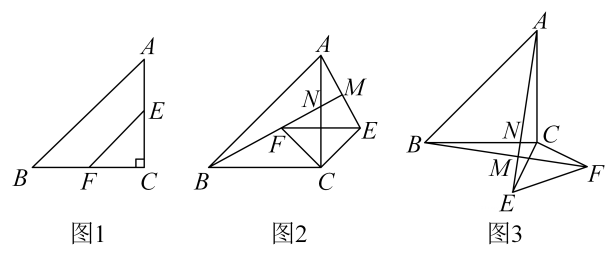
【问题提出】如图1，在
中，
， 点E，F分别为边AC，BC的中点，将
绕点C顺时针旋转
， 连接AE，BF，试探究AE，BF之间存在怎样的数量关系和位置关系？
(1)
【特例探究】若
， 将绕点C顺时针旋转至图2的位置，直线BF与AE，AC分别交于点M，N．按以下思路完成填空（第一个空填推理依据，第二个空填数量关系，第三个空填位置关系）：
(2)
【猜想证明】若
， 绕点C顺时针旋转至图3的位置，直线AE与BF，BC分别交于点M，N，猜想AE与BF之间的数量关系与位置关系，并就图3所示的情况加以证明；
(3)
【拓展运用】若
， 
， 将绕点C顺时针旋转 ， 直线AE，BF相交于点M，当以点C，E，M，F为顶点的四边形是矩形时，请直接写出BM的长．
∵ ， E，F分别为AC，BC的中点，
∴ ，
∵ ，
∴ ，
∴（）
∴AEBF， ， 又∵
，
∴ ，
∴AEBM．
【考点】
相似三角形的判定与性质;
三角形全等的判定-SAS;
能力提升
真题演练
