1.
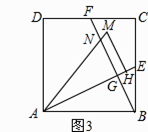
如图,点 、
、 、
、 、
、 在直线
在直线 上(
上( 、
、 之间不能直接测量),点
之间不能直接测量),点 、
、 在
在 异侧,测得
异侧,测得 ,
,  ,
,  .
.

(1)
求证: ;
(2)
若
;
(2)
若 ,
,  , 求
, 求 的长度.
的长度.
【考点】
三角形全等及其性质;
三角形全等的判定-ASA;
能力提升
真题演练