1.
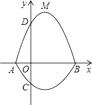
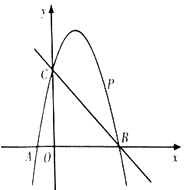
如图一所示,在平面直角坐标系中,抛物线 与
与 轴交于
轴交于 两点,与
两点,与 轴交于点
轴交于点 .
.

(1)
求抛物线的函数表达式及顶点坐标;
(2)
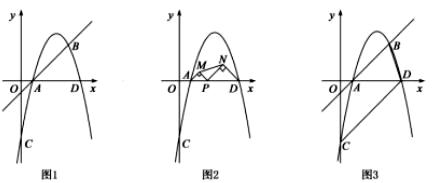
点 为第三象限内抛物线上一点,作直线
为第三象限内抛物线上一点,作直线 , 连接
, 连接 、
、 , 求
, 求 面积的最大值及此时点
面积的最大值及此时点 的坐标;
(3)
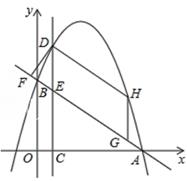
设直线
的坐标;
(3)
设直线 交抛物线于点
交抛物线于点 、
、 , 求证:无论
, 求证:无论 为何值,平行于
为何值,平行于 轴的直线
轴的直线 上总存在一点
上总存在一点 , 使得
, 使得 为直角.
为直角.
【考点】
二次函数与一次函数的综合应用;
二次函数的实际应用-几何问题;
能力提升
真题演练