1.
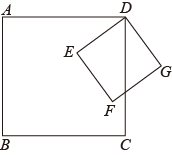
在△ABC中,AB=AC,∠BAC=90°,点D在射线BC上(与B、C两点不重合),以AD为边作正方形ADEF,使点E与点B在直线AD的异侧,射线BA与直线CF相交于点G.

(1)
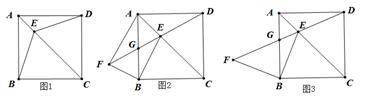
若点D在线段BC上,如图(1),判断:线段BC与线段CG的数量关系,位置关系;
(2)
如图(2),①若点D在线段BC的延长线上,(1)中判断线段BC与线段CG的数量关系与位置关系是否仍然成立,并说明理由;
②当G为CF中点,BC=2时,求线段AD的长.
【考点】
勾股定理;
正方形的性质;
三角形全等的判定-SAS;