1.
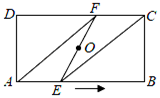
如图1，在矩形ABCD中，
， 
， 点E，F分别从点B，A出发，同时以每秒1cm的速度沿直线AB向左运动，当点E与点A重合时两点都停止运动，设运动时间为t秒．连接DF，CE，得到四边形CEFD．
(1)
当运动时间t为多少秒时，四边形CEFD是菱形？
(2)
如图2，在（1）的条件下，连接DE．将∠FDE绕点D逆时针旋转，在旋转过程中∠FDE的两边与线段FE，EC分别交于点M，N，连接MN．
①当时，旋转角∠FDM的度数为 ▲ 度，FM的长度为 ▲ cm；
②试探究线段MF，CN，MN之间的数量关系，并说明理由．
【考点】
菱形的判定与性质;
四边形-动点问题;
