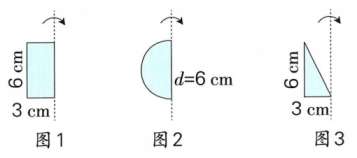
1.
积木是一种常见的儿童玩具,一套积木中通常有不同的颜色和形状。其中圆锥形积木是在圆柱形积木的基础上加工制作而成的。将一个底面半径是3cm、高是6cm的圆柱形积木加工制作成一个等底等高的圆锥形积木,加工制作过程中削去木料的体积是多少?(π取3.14)

【考点】
圆柱的体积(容积);
圆柱与圆锥体积的关系;
基础巩固
能力提升
变式训练
拓展培优
真题演练