1.
同学们根据“圆柱容球”设计了如下图所示的三个模型,请你思考并想象。
圆柱容球是古希腊数学家阿基米德的伟大发现之一。当圆柱容球时,球的直径与圆柱的高和底面直径相等。此时,球的体积是圆柱体积的三分之二。
|
(1)
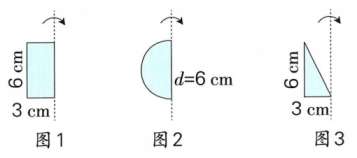
小雨将图1的长方形绕轴快速旋转一周,形成一个体,它的体积是cm3。
(2)
小浩将图2的半圆绕轴快速旋转一周,形成一个体,根据“圆柱容球”可知,它的体积是cm3。
(3)
小萱将图3的模型绕轴快速旋转一周,能形成一个形状如圆柱挖去一个等底、等高圆锥的几何体。她认为这个几何体的体积和图2的半圆绕轴快速旋转一周形成的几何体的体积相同,你同意她的看法吗?请说明理由。
【考点】
旋转与旋转现象;
圆柱的体积(容积);
球的认识及相关计算;
圆柱与圆锥体积的关系;

