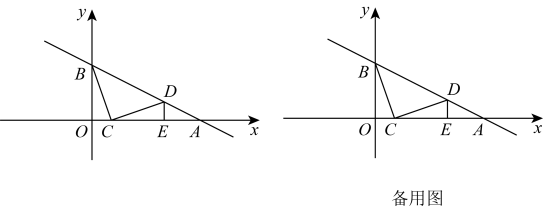
如图，在平面直角坐标系中，直线与x轴、y轴相交于A、B两点，动点C在线段上，将线段绕着点C顺时针旋转得到，此时点D恰好落在直线上时，过点D作轴于点E ．

0 返回出卷网首页

1. 如图，在平面直角坐标系中，直线 $\text{[math]}$ 与x轴、y轴相交于A、B两点，动点C在线段 $\text{[math]}$ 上，将线段 $\text{[math]}$ 绕着点C顺时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，此时点D恰好落在直线 $\text{[math]}$ 上时，过点D作 $\text{[math]}$ 轴于点E ．

(1) 求证： $\text{[math]}$ ；

(2) 求点D的坐标；

(3) 若点P在y轴上，点Q在直线 $\text{[math]}$ 上，是否存在以C、D、P、Q为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的Q点坐标；若不存在，请说明理由．

【考点】

坐标与图形性质; 一次函数的图象; 平行四边形的性质; 旋转的性质; 三角形全等的判定-AAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图1，在等边△ABC中，AB=6，点P、Q分别是边AB，AC 上的动点，满足AQ=2BP，以AP，AQ为邻边作平行四边形APDQ，PD，QD分别交 BC 于点E，F，设BP=m.

(1) CQ=（用含m的代数式表示）；

(2) 当平行四边形APDQ的面积为8 $\text{[math]}$ 时，求m的值；

(3) 如图2，连接PQ，线段CQ点绕Q点顺时针旋转90°得到C'Q，若点C'落在△APQ的内部（不包括边界）时，则m的取值范围为.

综合题困难

2. 如图，已知 $\text{[math]}$ 和点 $\text{[math]}$ ．将 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ．

(1) 在网格中画出 $\text{[math]}$ ．

(2) 若 $\text{[math]}$ ， $\text{[math]}$ 直接写出平行四边形 $\text{[math]}$ 的顶点 $\text{[math]}$ 的坐标．

综合题普通

3. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 在射线 $\text{[math]}$ 上（不与 $\text{[math]}$ ， $\text{[math]}$ 重合）， $\text{[math]}$ 交直线 $\text{[math]}$ 于点 $\text{[math]}$ ．

(1) 如图1，当点 $\text{[math]}$ 在线段 $\text{[math]}$ 上时，请直接写出 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系；

(2) 如图2，当点 $\text{[math]}$ 在线段 $\text{[math]}$ 的延长线上时，请写出 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系，并加以证明．

综合题普通