1.
为了市民游玩方便,准备在风阳湖市政森林公国内的环形路上提供免费游览车服务,如图是游览车路线图,已知 间的路程为
间的路程为 米,
米, 间的路程为
间的路程为 米,
米, 间的路程为
间的路程为 米,
米, 间的路程为
间的路程为 米,现有有
米,现有有 号,
号, 号两游览车分别从出口A和景点
号两游览车分别从出口A和景点 同时出发,
同时出发, 号车逆时针、
号车逆时针、 号车顺时针沿环形路连续循环行驶,供游客随时免费乘车(上,下车的时间忽略不计),两车速度均为
号车顺时针沿环形路连续循环行驶,供游客随时免费乘车(上,下车的时间忽略不计),两车速度均为 米/分.
米/分.

(1)
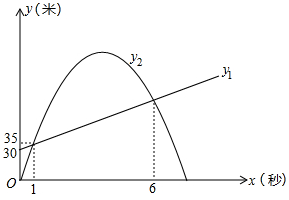
探究:设行驶时间为 分.
(2)
应用:已知游客小双在
分.
(2)
应用:已知游客小双在 上从景点
上从景点 向出口A走去,步行的速度是
向出口A走去,步行的速度是 米/分,当行进到
米/分,当行进到 上一点
上一点 (不与点
(不与点 , A重合)时,刚好与
, A重合)时,刚好与 号车迎面相遇,设
号车迎面相遇,设 的路程为s
的路程为s 米,写出他原地等候乘
米,写出他原地等候乘 号车到出口A所花时间
号车到出口A所花时间 与
与 的函数关系式,并直接写出
的函数关系式,并直接写出 在什么范围内时,等候乘
在什么范围内时,等候乘 号车能更快到达.
号车能更快到达.
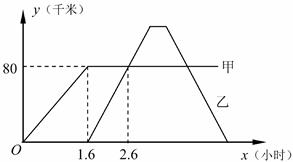
①当时,分别写出
号车,
号车在下半圈环线离出口A的路程
,
(米)与
(分)的函数关系式,并求出当两车相距的路程少于
米时
的取值范围;
②为何值时,
号车第三次恰好经过景点
, 并直接写出这一段时间内它与
号车相遇过的次数.
【考点】
一次函数的实际应用;