1.
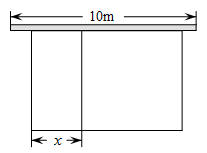
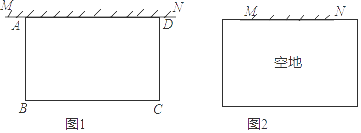
如图，要围一个矩形菜园ABCD，其中一边AD是墙，且AD的长不能超过26m，其余的三边AB、BC、CD用篱笆，且这三边的和为40m .
(1)
AB的长度是否能有两个不同的值都满足菜园面积为
说明理由.
(2)
当AB的长为多少时，围成的菜园面积最大?
【考点】
一元二次方程的应用-几何问题;
二次函数的实际应用-几何问题;
