1.
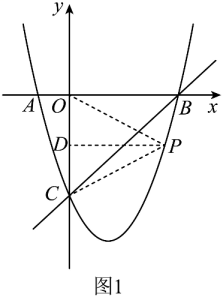
如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(-1,0),B(4,0),C(0,-4)三点,点P是直线BC下方抛物线上一动点.
(1)
求这个二次函数的解析式;
(2)
是否存在点P , 使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(3)
动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.
【考点】
二次函数图象与系数的关系;
二次函数的最值;
待定系数法求二次函数解析式;
线段垂直平分线的性质;