如图，四边形ABCD中，AB＝AD ， BC＝DC ，我们把这种两组邻边分别相等的四边形叫做“筝形”．

1. 如图，四边形ABCD中，AB＝AD ， BC＝DC ，我们把这种两组邻边分别相等的四边形叫做“筝形”．

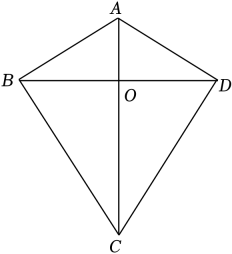
(1) 求证：△ABC≌△ADC；

(2) 测量OB与OD、∠BOA与∠DOA ，你有何猜想？证明你的猜想．

【考点】

三角形全等及其性质; 三角形全等的判定;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

解答题困难

2. 在 $\text{[math]}$ 中， $\text{[math]}$ 于点 $\text{[math]}$ ，且 $\text{[math]}$ ，在 $\text{[math]}$ 上取一点 $\text{[math]}$ ，使 $\text{[math]}$ 连接 $\text{[math]}$ ， $\text{[math]}$ ．

解答题普通

解答题普通