如图，在长方形ABCD中，点E在边AD上，将此长方形沿CE折叠，点D落在点F处，连接BF，B，F，E三点恰好在一直线上．

0 返回出卷网首页

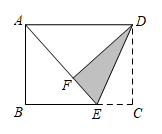
1. 如图，在长方形ABCD中，点E在边AD上，将此长方形沿CE折叠，点D落在点F处，连接BF，B，F，E三点恰好在一直线上．

(1) 求证：△BEC为等腰三角形；

(2) 若AE=CD，直接写出∠ECF的度数．

【考点】

等腰三角形的判定; 矩形的性质; 翻折变换（折叠问题）;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 小明将三角形纸片ABC（AB >AC）沿过点A的直线折叠，使得AC落在AB边上，折痕为AD，展开纸片（如图①）；再次折叠该三角形纸片，使点A和点D重合，折痕为EF，展平纸片后得到△AEF（如图②）．小明认为△AEF是等腰三角形，你同意吗？如果同意，请你给出证明，如果不同意，请说明理由．

解答题普通

2. 小明将三角形纸片 $\text{[math]}$ 沿过点 $\text{[math]}$ 的直线折叠，使得AC落在AB边上，折痕为AD，展开纸片(如图1)；再次折叠该三角形纸片，使点A和点D重合，折痕为EF，展平纸片后得到 $\text{[math]}$ (如图2).小明认为 $\text{[math]}$ 是等腰三角形，你同意他的说法吗?请你说明理由.

解答题普通

3. 如图，把一张长方形的纸ABCD沿EF折叠，重合部分是△MEF．问：△MEF是等腰三角形吗？为什么？

解答题普通