1.
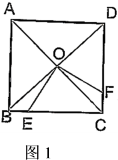
课本再现:如图正方形 对角线
对角线 与
与 相交于点O , E为
相交于点O , E为 上任意点(不与B , C重合),作
上任意点(不与B , C重合),作 交
交 于点F .
于点F .
(1)
在图1中解答下列问题:
(2)
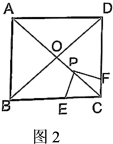
如图2,当点P为线段 上任意点时(P不与O , C重合),E , F为分别为边
上任意点时(P不与O , C重合),E , F为分别为边 上两点,且
上两点,且 . 问:
. 问: 之间有何数量关系,并说明理由.
(3)
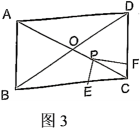
如图3,将图2中正方形
之间有何数量关系,并说明理由.
(3)
如图3,将图2中正方形 改成矩形
改成矩形 , 且
, 且 , 其它条件不变,直接写出
, 其它条件不变,直接写出 之间的数量关系.
之间的数量关系.
①)求证:
②)当正方形的面积为4时,小明发现以下结论:
①;②
;③
. 其中正确的是 (填序号)
【考点】
三角形全等及其性质;
勾股定理;
正方形的判定;
相似三角形的判定与性质;
等腰直角三角形;
四边形的综合;