1.
如图，正方形ABCD与正方形AEFG的边长分别为
和2，现在将正方形AEFG绕着点A旋转．
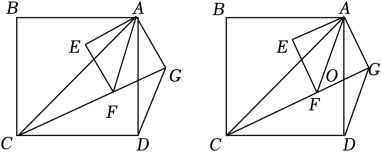
(1)
如图，连接CF、DG ， 求证：△ACF∽△ADG；
(2)
如图，连接CF ， 当点F在△ACD内，且∠ACF＝∠FAD时，设AD、FG的交点为O ， 求AO的长．
【考点】
三角形全等及其性质;
勾股定理;
正方形的性质;
相似三角形的判定与性质;
