如图1，△ABC和△ADE都是等边三角形，连接BD ， CE ．图1 图2

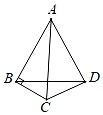
1. 如图1，△ABC和△ADE都是等边三角形，连接BD ， CE ．

图1 图2

(1) 证明：△ABD≌△ACE；

(2) 如图2，过点A作AP⊥BD于点P ，过点A作AQ⊥CE于点Q ．

证明：AP=AQ ．

【考点】

三角形的面积; 等边三角形的性质; 三角形全等的判定-SAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

解答题普通

2. 如图，在等边 $\text{[math]}$ 中，点P为 $\text{[math]}$ 内一点，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，以P为顶点作 $\text{[math]}$ ，且 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．

解答题普通

（Ⅰ）如图1，当PM＝AP，PN＝BP且∠APM＝∠BPN＝90°时，试猜想BM，AN之间的数量关系与位置关系，并证明你的猜想；

（Ⅱ）如图2，当△APM，△BPN都是等边三角形时，（Ⅰ）中BM，AN之间的数量关系是否仍然成立？若成立，请证明你的结论；若不成立，试说明理由．

（Ⅲ）在（Ⅱ）的条件下，连接AB得到图3，当PN＝2PM时，求∠PAB度数．

解答题普通