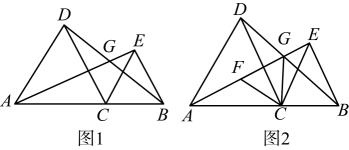
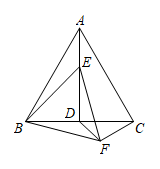
1.
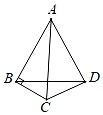
如图,在  中,以AB为边作等边△ABD(点C、D在边AB的同侧),连接CD.若∠ABC=90°,∠BAC=30°,求∠BDC的度数.
中,以AB为边作等边△ABD(点C、D在边AB的同侧),连接CD.若∠ABC=90°,∠BAC=30°,求∠BDC的度数.
【考点】
等边三角形的性质;
三角形全等的判定-SAS;
基础巩固
能力提升
变式训练
拓展培优
真题演练