1.
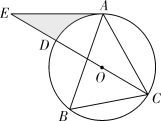
如图,在Rt△ABC中,∠ACB=90°,以AB为直径作⊙O,过点C作直线CD交AB的延长线于点D,并使∠BCD=∠A.求证:CD是⊙O的切线.

【考点】
等腰三角形的性质;
圆周角定理;
切线的判定;
基础巩固
能力提升
变式训练
拓展培优