1.
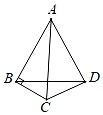
如图, 是等边三角形,
是等边三角形, . 动点
. 动点 从点
从点 出发,以
出发,以 速度沿射线
速度沿射线 运动. 连接
运动. 连接 , 以
, 以 为边向其右侧作等边三角形
为边向其右侧作等边三角形 , 连接
, 连接 . 设点
. 设点 的运动时间为
的运动时间为 (
( ).
).
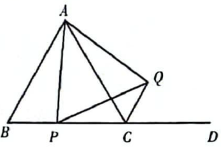
(1)
当点 在边
在边 上时,求
上时,求 的长;(用含
的长;(用含 的式子表示)
(2)
用含
的式子表示)
(2)
用含 的式子表示
的式子表示 的长;
(3)
当以点
的长;
(3)
当以点 为顶点的四边形是轴对称图形时,直接写出
为顶点的四边形是轴对称图形时,直接写出 的值.
的值.
【考点】
等边三角形的性质;
轴对称的性质;
三角形全等的判定-SAS;
三角形-动点问题;