0 返回出卷网首页
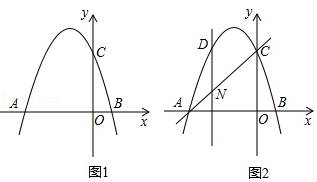
1. 抛物线与x轴交于点A，B（A在B左边），与轴交于点C，且OB＝2OC．

(1) 求抛物线的解析式；
(2) 若点P在第四象限的抛物线上，且∠PAB＝∠CBO，求点P的坐标；
(3) 若点D在x轴正半轴上且 ， 经过点D的直线MN交抛物线于点M，N（M在第一象限，N在第三象限），且满足 ， 求MN的解析式．
【考点】
一元二次方程的根与系数的关系（韦达定理）; 待定系数法求二次函数解析式; 相似三角形的判定与性质; 二次函数与一次函数的综合应用; 二次函数图象上点的坐标特征;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 困难
能力提升
换一批
1. 已知抛物线y＝x2+bx+c与x轴交于A（-1，0）、B两点，与y轴交于点C，OC=3OA，D为抛物线的顶点.

(1) 求抛物线的解析式；
(2) 若点P在抛物线上，tan∠ACP= ，求P点的坐标；
(3) 将抛物线沿直线y=x+b翻折，若点D的对应点E落在△ABC的内部（含△ABC的边）时，求b的取值范围.
综合题 困难
2. 已知二次函数y＝ax2+bx+c（a≠0）的图象与x轴交于A（﹣3，0），B（1，0）两点，与y轴交于点C（0，﹣3m）（m＞0），顶点为D.

(1) 如图1，当m＝1时，

①求该二次函数的解析式；

②点P为第三象限内的抛物线上的一个动点，连接AC、OP相交于点Q，求 的最大值；
(2) 如图2，当m取何值时，以A、D、C为顶点的三形与△BOC相似.
综合题 困难
3. 如图1，抛物线y＝﹣x2+mx+n交x轴于点A(﹣2，0)和点B，交y轴于点C(0，2).

(1) 求抛物线的函数表达式；
(2) 若点M在抛物线上，且S△AOM＝2S△BOC ， 求点M的坐标；
(3) 如图2，设点N是线段AC上的一动点，作DN⊥x轴，交抛物线于点D，求线段DN长度的最大值.
综合题 困难