1.
如图
(1)
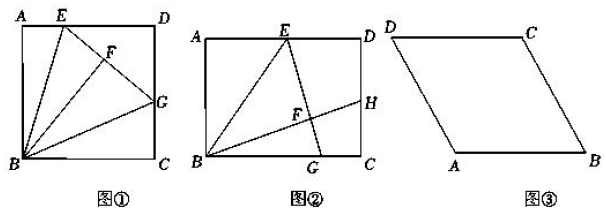
发现:如图①所示,在正方形 中,
中, 为
为 边上一点,将
边上一点,将 沿
沿 翻折到
翻折到 处,延长
处,延长 交
交 边于
边于 点.求证:
点.求证: ;
(2)
探究:如图②,在矩形
;
(2)
探究:如图②,在矩形 中,
中, 为
为 边上一点,且
边上一点,且 ,
,  . 将
. 将 沿
沿 翻折到
翻折到 处,延长
处,延长 交
交 边于
边于 点,延长
点,延长 交
交 边于点
边于点 , 且
, 且 , 求
, 求 的长.
(3)
拓展:如图③,在菱形
的长.
(3)
拓展:如图③,在菱形 中,
中, ,
,  为
为 边上的三等分点,
边上的三等分点, . 将
. 将 沿
沿 翻折得到
翻折得到 , 直线
, 直线 交
交 于点
于点 , 求
, 求 的长.
的长.
【考点】
直角三角形全等的判定-HL;
勾股定理;
正方形的性质;
翻折变换(折叠问题);
相似三角形的判定与性质;
能力提升


