1.
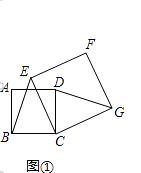
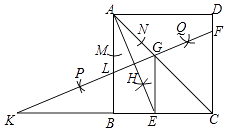
在正方形ABCD中, 为CD中点,连接AE并延长交BC延长线于点
为CD中点,连接AE并延长交BC延长线于点 , 点
, 点 在BC上,
在BC上, , 连接FE并延长交AD延长线于点
, 连接FE并延长交AD延长线于点 , 连接HG.
, 连接HG.

(1)
求证:四边形AFCH为菱形;
(2)
若DH=2,求四边形AFCH的面积.
【考点】
菱形的判定与性质;
正方形的性质;
相似三角形的判定与性质;