1.
(1)
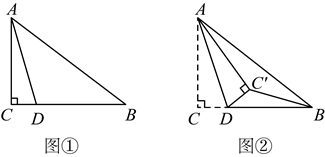
【感知】如图①,在 中,
中, , 点D为边
, 点D为边 上的一点,连接
上的一点,连接 . 若
. 若 是等腰三角形,
是等腰三角形, ,
,  , 则
, 则 的长为;
(2)
【探究】如图②,将
的长为;
(2)
【探究】如图②,将 沿
沿 翻折,得到
翻折,得到 , 连接
, 连接 . 若
. 若 是以
是以 为直角边的直角三角形,
为直角边的直角三角形, ,
,  , 求
, 求 的长.
的长.
【考点】
等腰三角形的性质;
勾股定理;
勾股定理的应用;
正方形的性质;
翻折变换(折叠问题);
能力提升


