1.
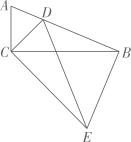
如图,在 中,
中, , M是斜边
, M是斜边 的中点,
的中点, , 垂足为点N , 且
, 垂足为点N , 且 的延长线交
的延长线交 于点D.
于点D.

(1)
求证 ;
(2)
如果
;
(2)
如果 , 求
, 求 的长度.
的长度.
【考点】
勾股定理;
相似三角形的判定与性质;