1.
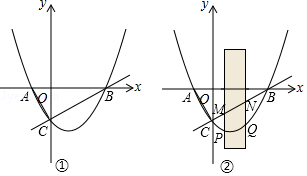
如图,一次函数 与
与 轴交于点
轴交于点 , 与
, 与 轴交于点
轴交于点 , 抛物线
, 抛物线 经过点
经过点 、
、 , 并与
, 并与 轴交于另一点
轴交于另一点 .
.

(1)
点 的坐标是,点
的坐标是,点 的坐标是;
(2)
求抛物线的解析式;
(3)
在直线
的坐标是;
(2)
求抛物线的解析式;
(3)
在直线 下方的抛物线上有一个点
下方的抛物线上有一个点 , 求这个四边形
, 求这个四边形 面积的最大值,并写出点
面积的最大值,并写出点 坐标;
(4)
在
坐标;
(4)
在 轴上有一个动点
轴上有一个动点 , 当线段
, 当线段 绕点
绕点 逆时针旋转
逆时针旋转 后得到线段
后得到线段 当线段
当线段 与抛物线只有一个公共点时,请直接写出
与抛物线只有一个公共点时,请直接写出 的取值范围.
的取值范围.
【考点】
二次函数与一次函数的综合应用;
二次函数-动态几何问题;
二次函数与一元二次方程的综合应用;
能力提升