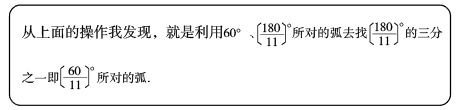
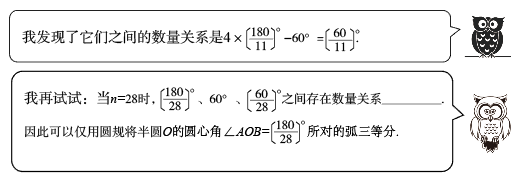
1.
综合与实践
定义:能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.
探索发现:用大小不同的圆形纸片去覆盖一张三角形纸片,经过多次操作发现:


①锐角三角形(和直角三角形)的最小覆盖圆是其外接圆,
②钝角三角形的最小覆盖圆是以其最长边为直径的圆.
如图1,以斜边AB为直径作圆,刚好是可以把Rt△ABC覆盖的面积最小的圆,称之为该直角三角形的最小覆盖圆.
(1)
实践与操作:如图2.在△ABC中,∠A=105°,试用直尺和圆规作出这个三角形的最小覆盖圆(不写作法,保留作图痕迹).
(2)
应用与计算:如图3,在△ABC中,∠A=80°,∠B=40°,AB , 请求出△ABC的最小覆盖圆的半径.
, 请求出△ABC的最小覆盖圆的半径.
【考点】
圆的综合题;
能力提升
真题演练