1.

(1)
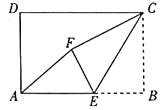
【初步探究】把矩形纸片 如图①折叠,当点B的对应点
如图①折叠,当点B的对应点 在
在 的中点时,填空:
的中点时,填空:
 (“
(“ ”或“
”或“ ”).
(2)
【类比探究】
(3)
【问题解决】
”).
(2)
【类比探究】
(3)
【问题解决】
如图②,当点B的对应点为
上的任意一点时,请判断(1)中结论是否成立?如果成立,请写出证明过程;如果不成立,请说明理由.
在矩形中,
, 点E为
中点,点P为线段
上一个动点,连接
, 将
沿
折叠得到
, 连接
, 当
为直角三角形时,
的长为.
【考点】
三角形全等的判定;
勾股定理;
矩形的性质;
翻折变换(折叠问题);
相似三角形的判定与性质;
能力提升
真题演练