请回忆华师版八年级上册数学教材第94页的部分内容，该内容阐述了垂直平分线的性质定理：线段垂直平分线上的点到线段两端钓距离相等；并给出了证明的方法。

0 返回出卷网首页

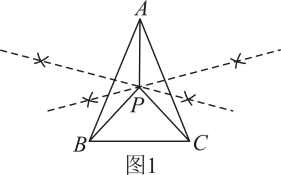
1. 请回忆华师版八年级上册数学教材第94页的部分内容，该内容阐述了垂直平分线的性质定理：线段垂直平分线上的点到线段两端钓距离相等；并给出了证明的方法。

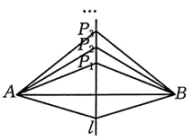
(1) 定理证明：根据教材的分析，结合图①，写出“线段垂直平分线的性质定理”完整的证明过程．

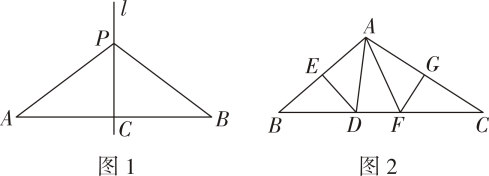
(2) 定理应用：如图②，在△ABC中，直线m、n分别是边BC、AC的垂直平分线，直线m、n交于点O ，过点O作OH⊥AB于点H ．求证：AH=BH ．

(3) 如图③，在△ABC中，AB=BC ，边AB的垂直平分线交AC于点D ，边BC的垂直平分线交AC于点E ．若∠ABC=120°，AC=9，求DE的值是多少？

【考点】

三角形全等及其性质; 三角形全等的判定; 线段垂直平分线的性质; 等腰三角形的性质; 等边三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

实践探究题普通

1. 综合与实践

在等腰三角形纸片 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ．现要将其剪成三张小纸片，使每张小纸片都是等腰三角形（不能有剩余）．下面是小文借助尺规解决这一问题的过程，请阅读后完成相应的任务．

作法：如图1．

①分别作 $\text{[math]}$ ， $\text{[math]}$ 的垂直平分线，交于点P；

②连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$

结论：沿线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 剪开，即可得到三个等腰三角形

理由：∵点P在线段 $\text{[math]}$ 的垂直平分线上，

∴____．（依据）

同理，得 $\text{[math]}$

∴ $\text{[math]}$

∴ $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 都是等腰三角形．

任务：

(1) 上述过程中，横线上的结论为，括号中的依据为．

(2) 受小文的启发，同学们想到另一种思路：如图2，以点B为圆心， $\text{[math]}$ 长为半径作弧，交 $\text{[math]}$ 于点D，交 $\text{[math]}$ 于点E．在此基础上构造两条线段（以图中标有字母的点为端点）作为裁剪线，也可解决问题．请在图2中画出一种裁剪方案，并求出得到的三个等腰三角形及相应顶角的度数．

(3) 如图3，在等腰三角形纸片 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ．请在图3中设计出一种裁剪方案，将该三角形纸片分成三个等腰三角形．（要求：尺规作图，保留作图痕迹，不写作法，说明裁剪线）

实践探究题普通

2. △ABC是等边三角形，点D是AC边上动点，∠CBD＝α（0°＜α＜30°），把△ABD沿BD对折，得到△A^'BD．

(1) 如图1，若α＝15°，则∠CBA^'＝　　．

(2) 如图2，点P在BD延长线上，且∠DAP＝∠DBC＝α．

①试探究AP，BP，CP之间是否存在一定数量关系，猜想并说明理由．

②若BP＝10，CP＝m，求CA^'的长．（用含m的式子表示）

实践探究题困难

3. 课本再现

如图，直线l垂直平分线段AB ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， …是l上的点，分别量一量点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， …到点A与点B的距离，你有什么发现？可以发现，点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， …到点A的距离与它们到点B的距离分别相等.

(1) 定理证明

为了证明该性质，珍珍画出了图形，并写出了“已知”和“求证”，请你完成证明过程.

已知：如图1，直线 $\text{[math]}$ ，垂足为C ， $\text{[math]}$ ，点P在直线l上，求证： $\text{[math]}$ .

(2) 知识应用

如图2，在 $\text{[math]}$ 中， $\text{[math]}$ ， DE ， FG分别是边AB ， AC的垂直平分线，与 $\text{[math]}$ 的交点分别为D ， E ， F ， G ，连接AD ， AF ，求 $\text{[math]}$ 的周长.

实践探究题普通