1.
在矩形 中,已知
中,已知 , 连接
, 连接 , 点
, 点 是边
是边 上的一动点,
上的一动点, 的半径为定值
的半径为定值 .
.

图1 图2 图3
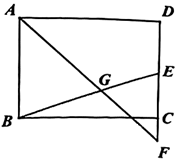
(1)
如图1,当 经过点
经过点 时,恰好与
时,恰好与 相切,求
相切,求 的半径
的半径 ;
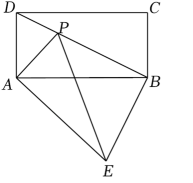
(2)
如图2,点
;
(2)
如图2,点 是
是 上的一动点,求三角形
上的一动点,求三角形 面积的最大值;
(3)
若
面积的最大值;
(3)
若 从
从 出发,沿
出发,沿 方向以每秒一个单位长度向
方向以每秒一个单位长度向 点运动,同时,动点
点运动,同时,动点 分别从点
分别从点 , 点
, 点 出发,其中点
出发,其中点 沿着
沿着 方向向点
方向向点 运动,速度为每秒1个单位长度,点
运动,速度为每秒1个单位长度,点 沿着射线
沿着射线 方向运动,速度为每秒2个单位长度,连接
方向运动,速度为每秒2个单位长度,连接 , 如图3所示,当
, 如图3所示,当 平移至点
平移至点 (圆心
(圆心 与点
与点 重合)时停止运动,点
重合)时停止运动,点 也随之停止运动.设运动时间为
也随之停止运动.设运动时间为 (秒).在运动过程中,是否存在某一时间
(秒).在运动过程中,是否存在某一时间 , 使
, 使 与
与 相切,若存在,请求出此时
相切,若存在,请求出此时 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【考点】
含30°角的直角三角形;
勾股定理;
矩形的性质;
切线的性质;
相似三角形的判定与性质;
能力提升