1.
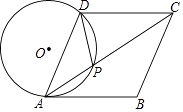
四边形 是菱形,点O为对角线交点,
是菱形,点O为对角线交点, 边的垂直平分线交线段
边的垂直平分线交线段 于点P(P不与O重合),连接
于点P(P不与O重合),连接 , 以点P为圆心,
, 以点P为圆心, 长为半径的圆交直线
长为半径的圆交直线 于点E,直线
于点E,直线 与直线
与直线 交于点F,如图所示.
交于点F,如图所示.

(1)
当 时,求证:直线
时,求证:直线 与
与 相切;
(2)
当
相切;
(2)
当 ,
,  时,求
时,求 的度数;
(3)
在菱形
的度数;
(3)
在菱形 的边长与内角发生变化的过程中,若点C与E不重合,请探究
的边长与内角发生变化的过程中,若点C与E不重合,请探究 与
与 的数量关系.
的数量关系.
【考点】
菱形的性质;
切线的判定与性质;
能力提升
真题演练