1.
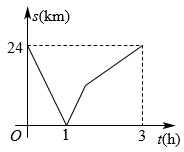
【素材1】某景区游览路线及方向如图1所示,①、④、⑥各路段路程相等,⑤、⑦、⑧各路段路程相等,②、③两路段路程相等.
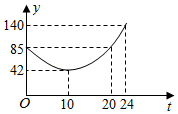
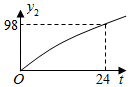
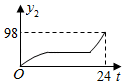
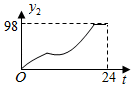
【素材2】设游玩行走速度恒定,经过每个景点都停留20分钟.小温游路线①、④、⑤、⑥、⑦、⑧用时3小时25分钟;小州游路线①、②、⑧,他离入口的路程与时间
的关系(部分数据)如图2所示,在离入口2100米处,他到出口还要走10分钟.

【问题】路线①、③、⑥、⑦、⑧路程之和为( )
A.
4200米
B.
4800米
C.
5200米
D.
5400米
【考点】
函数的图象;
通过函数图象获取信息;