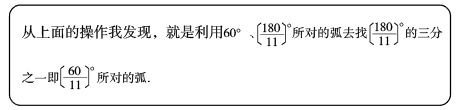
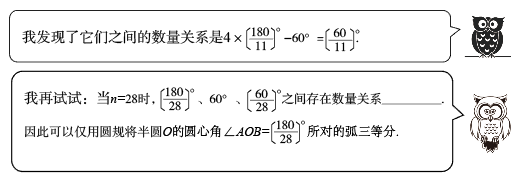
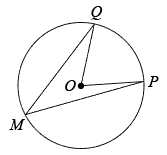
1.
联想与思考
【提出问题】同学们已经研究过锐角三角形面积与内切圆半径之间的关系，即：如图1，在锐角中，
、
、
的对边分别是
、
、
， 设
的内切圆
半径为
，
的面积为
， 则
.小明同学在学习了以上的知识后提出了另一个问题：任意一个锐角三角形都有内切圆与外接圆，那么锐角三角形的面积
与它的外接圆半径有怎样的关系呢？
图1
【分析问题】为解决该问题，老师让同学们进行了如下的思考与探究：
(1)
如图2，设锐角
的外接圆半径为
， 同学们得出猜想：
.
(2)
请你根据上述启发，结合图3，证明：
.
(3)
【解决问题】
在证明的过程中，同学们发现该猜想的结论与有关，由此启发：添加辅助线构建直角三角形来解决问题.小明经过思考做了以下尝试解答，请你补全证明过程：
连接
|
图2 图3
结合（1）、（2）的结论，请探究出锐角三角形的面积与它的外接圆半径
之间的关系（用含有
、
、
和
的式子表示
），并说明理由.
【考点】
三角形的面积;
圆的综合题;
锐角三角函数的定义;
能力提升
真题演练
