1.
数学活动:如何提高篮球运动罚球命中率——以小华同学为例
活动背景:某学校体育节进行班级篮球比赛,在训练过程中发现小华同学罚球命中率较低,为帮助小华同学提高罚球命中率,该班数学小组拍摄了如图1片并测量了相应的数据(图片标注的是近似值).
活动背景:某学校体育节进行班级篮球比赛,在训练过程中发现小华同学罚球命中率较低,为帮助小华同学提高罚球命中率,该班数学小组拍摄了如图1片并测量了相应的数据(图片标注的是近似值).



(1)
模型建立:如图2所示,直线AE是地平线,A为小华罚球时脚的位置,篮球在运动过程中B、D、F为篮球的三个不同位置,B点为球出手时候的位置.已知AB=1.75m,CD=3.202m,EF=3.042m,AC=2.2m,AE=3.8m,篮球运动轨迹是抛物线的一部分,数学小组以A、B、C、D、E、F中的某一点为原点,水平方向为x轴,竖直方向为y轴建立平面直角坐标系,计算出篮球的运动轨迹对应的抛物线解析式为  , 根据解析式,请你判断该数学小组是以点(填A、B、C、D、E、F中的一个)作为坐标原点
(2)
问题解决:已知篮球框与罚球线水平距离为4米,距离地面为3米,请问在(1)的情况下,小华的这次罚球能否罚进?并说明理由.
(3)
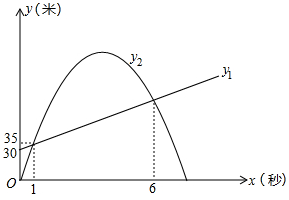
模型应用:如下图所示为抛物线
, 根据解析式,请你判断该数学小组是以点(填A、B、C、D、E、F中的一个)作为坐标原点
(2)
问题解决:已知篮球框与罚球线水平距离为4米,距离地面为3米,请问在(1)的情况下,小华的这次罚球能否罚进?并说明理由.
(3)
模型应用:如下图所示为抛物线 的 一部分函数图象,抛物线外一点P(4,3),试通过计算说明在不改变抛物线形状的情况下,把原抛物线向上平移多少个单位,能使平移后的抛物线经过点P.
的 一部分函数图象,抛物线外一点P(4,3),试通过计算说明在不改变抛物线形状的情况下,把原抛物线向上平移多少个单位,能使平移后的抛物线经过点P.
【考点】
二次函数的实际应用-抛球问题;
能力提升
真题演练