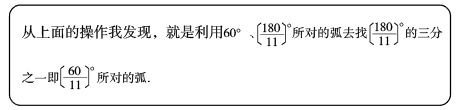
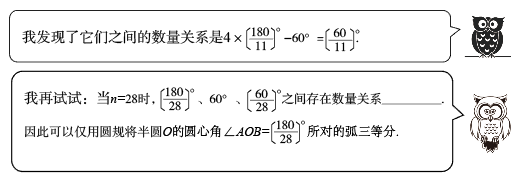
【教材呈现】现行人教版九年级下册数学教材85页“拓广探索”第14题：14．如图，在锐角中，探究，，之间的关系．（提示：分别作和边上的高．）【得出结论】．

1. 【教材呈现】

现行人教版九年级下册数学教材85页“拓广探索”第14题：

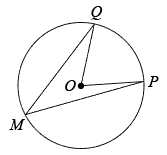
14．如图，在锐角 $\text{[math]}$ 中，探究 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的关系．（提示：分别作 $\text{[math]}$ 和 $\text{[math]}$ 边上的高．）

【得出结论】

$\text{[math]}$ ．

(1) 【基础应用】

在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，利用以上结论求 $\text{[math]}$ 的长；

(2) 【推广证明】

进一步研究发现， $\text{[math]}$ 不仅在锐角三角形中成立，在任意三角形中均成立，并且还满足 $\text{[math]}$ （R为 $\text{[math]}$ 外接圆的半径）．请利用图1证明： $\text{[math]}$ ．

(3) 【拓展应用】

如图2，四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．求过A ， B ， D三点的圆的半径．

【考点】

矩形的判定与性质; 圆的综合题; 锐角三角函数的定义;

【答案】

您现在未登录，无法查看试题答案与解析。登录

实践探究题困难

1. 操作探究题

(1) 已知 $\text{[math]}$ 是半圆 $\text{[math]}$ 的直径， $\text{[math]}$ （ $\text{[math]}$ 是正整数，且 $\text{[math]}$ 不是3的倍数）是半圆 $\text{[math]}$ 的一个圆心角．

操作：如图1，分别将半圆 $\text{[math]}$ 的圆心角 $\text{[math]}$ （ $\text{[math]}$ 取1、4、5、10）所对的弧三等分（要求：仅用圆规作图，不写作法，保留作图痕迹）；

交流：当 $\text{[math]}$ 时，可以仅用圆规将半圆 $\text{[math]}$ 的圆心角 $\text{[math]}$ 所对的弧三等分吗？

探究：你认为当 $\text{[math]}$ 满足什么条件时，就可以仅用圆规将半圆 $\text{[math]}$ 的圆心角 $\text{[math]}$ 所对的弧三等分？说说你的理由．

(2) 如图2， $\text{[math]}$ 的圆周角 $\text{[math]}$ ．为了将这个圆的圆周14等分，请作出它的一条14等分弧 $\text{[math]}$ （要求：仅用圆规作图，不写作法，保留作图痕迹）．

实践探究题普通

2. 综合与实践

定义：能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.

探索发现：用大小不同的圆形纸片去覆盖一张三角形纸片，经过多次操作发现：

①锐角三角形（和直角三角形）的最小覆盖圆是其外接圆，

②钝角三角形的最小覆盖圆是以其最长边为直径的圆.

如图1，以斜边AB为直径作圆，刚好是可以把Rt△ABC覆盖的面积最小的圆，称之为该直角三角形的最小覆盖圆.

(1) 实践与操作：如图2．在△ABC中，∠A＝105°，试用直尺和圆规作出这个三角形的最小覆盖圆（不写作法，保留作图痕迹）．

(2) 应用与计算：如图3，在△ABC中，∠A＝80°，∠B＝40°，AB $\text{[math]}$ ，请求出△ABC的最小覆盖圆的半径．

实践探究题普通

3. 问题发现

(1) 在△ABC中，AB＝2，∠C＝60°，则△ABC面积的最大值为；

(2) 如图1，在四边形ABCD中，AB＝AD＝6，∠BCD＝∠BAD＝90°，AC＝8，求BC+CD的值．

(3) 问题解决

有一个直径为60cm的圆形配件⊙O，如图2所示．现需在该配件上切割出一个四边形孔洞OABC，要求∠O＝∠B＝60°，OA＝OC，并使切割出的四边形孔洞OABC的面积尽可能小．试问，是否存在符合要求的面积最小的四边形OABC？若存在，请求出四边形OABC面积的最小值及此时OA的长；若不存在，请说明理由．

实践探究题困难