1.
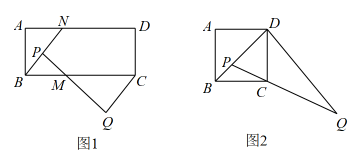
在学习特殊的平行四边形时，我们发现正方形的对角线等于边长的
倍，某数学兴趣小组以此为方向对菱形的对角线和边长的数量关系探究发现，具体如下：如图1．
(1)
∵四边形ABCD是菱形，
(2)
[类比探究]
(3)
[拓展应用]
∴AC⊥BD ， AO＝CO ， BO＝DO ．
∴AB2＝AO2+BO2
又∵AC＝2AO ， BD＝2BO ，
∴AB2＝+．
化简整理得AC2+BD2＝．
如图2，若四边形ABCD是平行四边形，请说明边长与对角线的数量关系．
如图3，四边形ABCD为平行四边形，对角线AC ， BD相交于点O ， 点E为AO的中点，点F为BC的中点，连接EF ， 若AB＝8，BD＝8，AC＝12，直接写出EF的长度．
【考点】
三角形全等及其性质;
勾股定理;
相似三角形的判定与性质;
三角形全等的判定-AAS;
四边形的综合;
能力提升
