组卷在线网-ZUJUAN.COM

0 返回出卷网首页

1.

(1) 【甚础巩固】

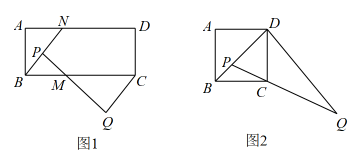
如图（1），在△ABC和△EDB中，点E在BC上，AC∥BD ， ∠A＝∠BED ，求证：△ABC∽△EDB ．

(2) 【尝试应用】

如图（2），在（1）的条件下，连结CD ．若∠BCD＝90°，AC＝EC＝2，BE＝4，求DE的长．

(3) 【拓展提高】

如图（3），在▱ABCD中，对角线AC ， BD相交于点O ，点E是边CD上一点，DE＝2CE ，连结AE交BD于点F ，线段AE与BC的延长线交于点P ，若∠AFB＝∠ABC ， OF＝1，求BC的长．

【考点】

勾股定理; 平行四边形的性质; 相似三角形的判定与性质; 四边形的综合;

【答案】

您现在未登录，无法查看试题答案与解析。登录

实践探究题困难

(1) 【基础巩固】如图1，在△ABC中，D，E，F分别为AB，AC，BC上的点，DE//BC，BF=CF，AF交DE于点G，求证：DG=EG.

(2) 【尝试应用】如图2，在（1）的条件下，连接CD，CG.若CG⊥DE，CD=10，AE=6，求 $\text{[math]}$ 的值.

(3) 【拓展提高】如图3，在 $\text{[math]}$ ABCD中，∠ADC=45°，AC与BD交于点O，E为AO上一点，EG//BD交AD于点G，EF⊥EG交BC于点F.若∠EGF=40°，FG平分∠EFC，FG=8，求BF的长.

实践探究题困难

(1) 【基础巩固】

如图①，在△ABC中，D，E，F 分别为AB，AC，BC上的点，DE∥BC，BF=CF，AF 交DE 于点G.求证：DG=EG.

(2) 【尝试应用】

如图②，在（1）的条件下，连结CD，CG.若CG⊥DE，CD=6，AE=3，求DE的值.

(3) 【拓展提高】

如图③，在▱ABCD中， $\text{[math]}$ AC 与BD 相交于点O，E为AO上一点，EG∥BD交AD于点G，EF⊥EG交BC于点F.若∠EGF=40°，FG 平分∠EFC，FG=10，求BF的长。

实践探究题困难

3. 【问题背景】如图1，在矩形 $\text{[math]}$ 中，点M，N分别在边 $\text{[math]}$ ， $\text{[math]}$ 上，且 $\text{[math]}$ ，连接 $\text{[math]}$ ，点P在 $\text{[math]}$ 上，连接 $\text{[math]}$ 并延长至点Q，使 $\text{[math]}$ ，连接 $\text{[math]}$ .

(1) 【尝试初探】求证： $\text{[math]}$ ；

(2) 【深入探究】若 $\text{[math]}$ ， $\text{[math]}$ ，点P为 $\text{[math]}$ 中点，连接 $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$ ；

(3) 【拓展延伸】如图2，在正方形 $\text{[math]}$ 中，点P为对角线 $\text{[math]}$ 上一点，连接 $\text{[math]}$ 并延长至点Q，使 $\text{[math]}$ ，连接 $\text{[math]}$ ，若 $\text{[math]}$ ，求 $\text{[math]}$ 的值（用含n的代数式表示）

实践探究题困难