1.
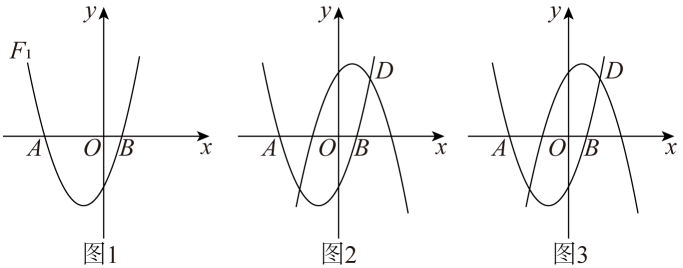
如图,抛物线 交
交 轴于点
轴于点 , 点
, 点 , 与
, 与 轴交于点
轴交于点 .
.

(1)
求抛物线的表达式;
(2)
点 为直线
为直线 下方抛物线上的一点,过点
下方抛物线上的一点,过点 作
作 轴交
轴交 于点
于点 , 作
, 作 轴交
轴交 于点
于点 , 求
, 求 的最大值以及此时点
的最大值以及此时点 的坐标;
(3)
将原抛物线沿射线
的坐标;
(3)
将原抛物线沿射线 方向平移
方向平移 个单位长度得到新抛物线
个单位长度得到新抛物线 , 点
, 点 是新抛物线
是新抛物线 上的一个动点,连接
上的一个动点,连接 , 将
, 将 沿着直线
沿着直线 翻折到同一平面内得到
翻折到同一平面内得到 , 连接
, 连接 , 当∠
, 当∠ 时,直接写出点
时,直接写出点 的坐标,并写出求解其中一个坐标的过程.
的坐标,并写出求解其中一个坐标的过程.
【考点】
待定系数法求一次函数解析式;
二次函数图象的几何变换;
待定系数法求二次函数解析式;
能力提升
真题演练