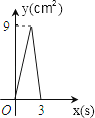1.
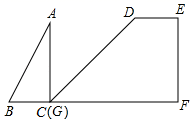
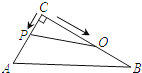
如图1,在正方形 中,动点P,Q同时从点A出发,以相同的速度分别沿A→B→C和A→D→C的路径向点C运动.设运动时间为x(单位:
中,动点P,Q同时从点A出发,以相同的速度分别沿A→B→C和A→D→C的路径向点C运动.设运动时间为x(单位: ),四边形
),四边形 的面积为y(单位:
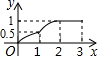
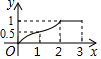
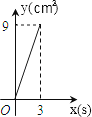
的面积为y(单位: ),y与x之间的函数图象如图2所示.
),y与x之间的函数图象如图2所示.

(1)
正方形的边长为 , 点P的运动速度为 ;
(2)
求y与x之间的函数关系式;
(3)
若P在 上运动时,点P,Q的位置记为
上运动时,点P,Q的位置记为 , 若P在BC上运动时,点P,Q的位置记为
, 若P在BC上运动时,点P,Q的位置记为 , 且点P从
, 且点P从 运动到
运动到 的距离为
的距离为 , 求六边形
, 求六边形 面积的最大值.
面积的最大值.
【考点】
二次函数-动态几何问题;
动点问题的函数图象;
能力提升
真题演练