我们将内角互为对顶角的两个三角形称为“对顶三角形”．例如，在图1中，△AOB的内角∠AOB与△COD的内角∠COD互为对顶角，则△AOB与△COD为“对顶三角形”，根据三角形内角和定理知“对顶三角形”有如下性质：∠A+∠B=∠C+∠D．

0 返回出卷网首页

1. 我们将内角互为对顶角的两个三角形称为“对顶三角形”．例如，在图1中，△AOB的内角∠AOB与△COD的内角∠COD互为对顶角，则△AOB与△COD为“对顶三角形”，根据三角形内角和定理知“对顶三角形”有如下性质：∠A+∠B=∠C+∠D．

(1) 如图1，在“对顶三角形”△AOB与△OOD中，∠AOB=70°，则∠C+∠D= °．

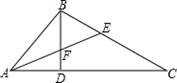
(2) 如图2，在△ABC中，AD、BE分别平分∠BAC和∠ABC，若∠C=60°，∠ADE比∠BED大6°，求∠BED的度数．

【考点】

三角形内角和定理; 角平分线的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题困难

1. 如图，DB是△ABC的高，AE是角平分线，∠BAE＝26°，求∠BFE的度数．

解答题普通

2. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ ．求 $\text{[math]}$ 和 $\text{[math]}$ 的度数．

解答题普通

3. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ．求 $\text{[math]}$ ， $\text{[math]}$ 的度数．

解答题普通