1.
如图1,在 中,
中, ,
,  ,
,  厘米,点
厘米,点 从点
从点 开始沿
开始沿 边向点
边向点 以每秒2厘米的速度移动,同时点
以每秒2厘米的速度移动,同时点 从点
从点 开始沿
开始沿 边向点
边向点 以每秒1厘米的速度移动,其中任意一点到达目的地后,两点同时停止运动.求:
以每秒1厘米的速度移动,其中任意一点到达目的地后,两点同时停止运动.求:

(1)
点 从点
从点 出发,经过几秒
出发,经过几秒 的面积等于1平方厘米?
(2)
是否存在以点
的面积等于1平方厘米?
(2)
是否存在以点 为圆心、
为圆心、 为半径的圆与直线
为半径的圆与直线 相切,若存在,求出经过几秒相切?若不存在,请说明理由;
(3)
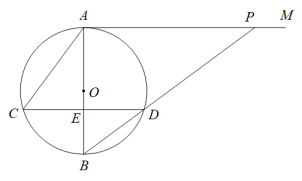
如图2,点
相切,若存在,求出经过几秒相切?若不存在,请说明理由;
(3)
如图2,点 是
是 内的一个动点,且满足
内的一个动点,且满足 , 求线段
, 求线段 的最小值.
的最小值.
【考点】
勾股定理;
圆周角定理;
切线的性质;